materi belajar, soal ,rpp matematika: Menyelesaikan Persamaan Kuadrat

gambar contoh persamaan kuadrat

Persamaan kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah
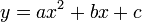
$y = ax^2 + bx + c \,\!$
dengan
$a \ne 0 \,\!$
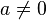
Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari $x^2$ , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.

Bentuk umum : ax² + bx + c = 0
x variabel; a,b,c konstanta ; a ¹ 0
Menyelesaikan persamaan kuadrat berarti mencari harga x yang memenuhi persamaan kudrat (PK) tersebut (disebut akar persamaan kuadrat). Suatu bilangan disebut akar dari suatu persamaan berarti bilangan tersebut memenuhi persamaan.
Andaikan x1 dan x2 adalah akar-akar persamaan kuadrat, maka x1 dan x2 dapat ditentukan dengan cara

Memfaktorkan

ax² + bx + c = 0 ® ax² + bx + c = 0 ® a (x + p/a) (x + p/a) = 0
® x1 = - p/a dan x2 = - q/a

dengan p.q = a.c dan p + q = b

Melengkapkan bentuk kuadrat
persamaan kuadrat tersebut dibentuk menjadi
(x + p)² = q² ® x + p = ± q
x1 = q - p dan x2 = - q - p

Rumus ABC
ax² + bx + c = 0 ® X1,2 = ( [-b ± Ö(b²-4ac)]/2a

bentuk (b² - 4ac) selanjutnya disebut DISKRIMINAN (D) sehingga
sehingga X1,2 = (-b ± ÖD)/2a

Arti nilai a, b, dan c

Variasi nilai a

Variasi nilai b

Variasi nilai c

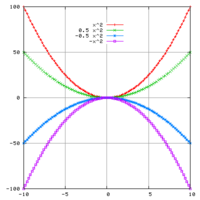
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.
a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a < 0 akan menyebabkan parabola terbuka ke bawah. b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a. c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.