- Himpunan bagian notasi : Ì atau ÉHimpunan A adalah himupnan bagian dari himpunan B, jika setiap anggota A adalah anggota B.Ditulis : A Ì Bf atau B É Acontoh:A={a,b}; B={a,b,c}; C={a,b,c,d}maka A Ì B ; A Ì C ; B Ì Cketentuan :
- himpunan kosong merupakan himpunan bagian dari sembarang
- himpunan ( f Ì A )himpunan A adalah himpunan bagian dari
- himpunan A sendiri ( A Ì A)jika anggota himpunan A ada sebanyak n, maka banyaknya himpunan bagian dari A adalah HB = 2n
HB = 2ncontoh:jika A = {a,b,c}maka himpunan bagian dari A adalah :{a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c} dan fseluruhnya ada 2³ = 8POWER SET 2shimpunan yang elemennya adalah himpunan-himpunan bagian dari Scontoh:S = {a,b,c}2s = { {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}, f } - Himpunan sama ttttttttttt notasi : =Dua himpunan A dan B adalah sama, jika setiap elemen A adalah elemen B, dan setiap elemen B adalah elemen A.Ditulis A = Bcontoh:K = {x | x²-3x+2=0}L = {2,1}maka K = L
- Himpunan lepas ttttttttttt notasi : //Dua himpunan A dan B disebut saling lepas, jika himpunan A tidak mempunyai anggota persekutuan dengan himpunan B.Ditulis A // Bcontoh:A = {a,b,c}B = {k,l,m}Maka A // B
Subhimpunan
Dari suatu himpunan, misalnya A = {apel, jeruk, mangga, pisang}, dapat dibuat himpunan-himpunan lain yang elemen-elemennya adalah diambil dari himpunan tersebut.
- {apel, jeruk}
- {jeruk, pisang}
- {apel, mangga, pisang}
Ketiga himpunan di atas memiliki sifat umum, yaitu setiap anggota himpunan itu adalah juga anggota himpunan A. Himpunan-himpunan ini disebut sebagai subhimpunan atauhimpunan bagian dari A. Jadi dapat dirumuskan:
B adalah himpunan bagian dari A jika setiap elemen B juga terdapat dalam A.
Kalimat di atas tetap benar untuk B himpunan kosong. Maka  juga subhimpunan dari A.
juga subhimpunan dari A.
 juga subhimpunan dari A.
juga subhimpunan dari A.
Untuk sembarang himpunan A,
Definisi di atas juga mencakup kemungkinan bahwa himpunan bagian dari A adalah A sendiri.
Untuk sembarang himpunan A,
Istilah subhimpunan dari A biasanya berarti mencakup A sebagai subhimpunannya sendiri. Kadang-kadang istilah ini juga dipakai untuk menyebut himpunan bagian dari A, tetapi bukan A sendiri. Pengertian mana yang digunakan biasanya jelas dari konteksnya.
Subhimpunan sejati dari A menunjuk pada subhimpunan dari A, tetapi tidak mencakup A sendiri.
[sunting]
Superhimpunan
Kebalikan dari subhimpunan adalah superhimpunan, yaitu himpunan yang lebih besar yang mencakup himpunan tersebut.
[sunting]
Kesamaan dua himpunan
Himpunan A dan B disebut sama, jika setiap anggota A adalah anggota B, dan sebaliknya, setiap anggota B adalah anggota A.
atau
Definisi di atas sangat berguna untuk membuktikan bahwa dua himpunan A dan B adalah sama. Pertama, buktikan dahulu A adalah subhimpunan B, kemudian buktikan bahwa Badalah subhimpunan A.
[sunting]
Himpunan Kuasa
Himpunan kuasa atau himpunan pangkat (power set) dari A adalah himpunan yang terdiri dari seluruh himpunan bagian dari A. Notasinya adalah  .
.
 .
.
Jika A = {apel, jeruk, mangga, pisang}, maka  :
:
 :
:{ { },{apel}, {jeruk}, {mangga}, {pisang},{apel, jeruk}, {apel, mangga}, {apel, pisang},{jeruk, mangga}, {jeruk, pisang}, {mangga, pisang},{apel, jeruk, mangga}, {apel, jeruk, pisang}, {apel, mangga, pisang}, {jeruk, mangga, pisang},{apel, jeruk, mangga, pisang} }
Banyaknya anggota yang terkandung dalam himpunan kuasa dari A adalah 2 pangkat banyaknya anggota A.



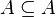



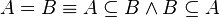

Tidak ada komentar:
Posting Komentar